The Crazy Frog Puzzle (CFP) is the following: we have a $n \times n$ partially filled board, a crazy frog placed on an empty cell and a sequence of horizontal, vertical, and diagonal jumps; each jump has a fixed length and two possible opposite directions. The crazy frog must follow the sequence of jumps, and at each step it can only choose among the two available directions. Can the frog visit every empty cell of the board exactly once (it cannot jump on a blocked cell and on the same cell two times)?

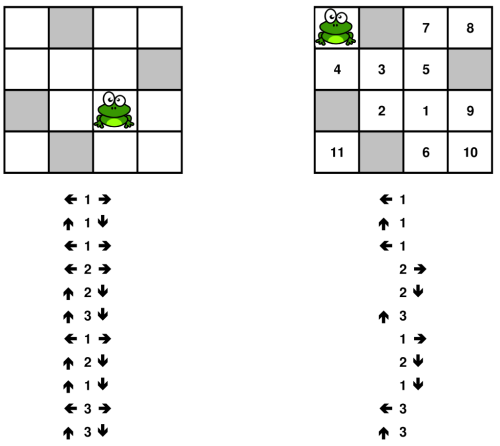 Figure 1: an example of the Crazy Frog Puzzle on the left and its solution on the right.

 We prove that the Crazy Frog Puzzle is $\sf{NP}$-complete even if restricted to 1 dimension and even without blocked cells. The 1-D CFP without blocked cells corresponds to the problem of reconstructing a permutation from its differences:

Permutation Reconstruction from Differences problem:
Input: a set of $n-1$ distances $a_1,a_2,…,a_{n-1}$
Question: does exist a permutation $\pi_1,…,\pi_n$ of the integers $[1..n]$ such that $| \pi_{i+1} – \pi_i| = a_i$, $i=1,…,n-1$ ?

For example, given the differences $(2,1,2,1,5,3,1,1)$ a valid permutation of $[1..9]$ is $(5,7,6,8,9,4,1,2,3)$

Update 2013-12-19: a new version of the paper is available.

click here to download a draft of the paper