I just bought the nice book “Problems with a POINT – Exploring Math and Computer Science” by William Gasarch and Clyde Kruskal. The book explains many nice mathematical and theoretical computer science problems that are “easy-to-understand-but-not-so-easy-to-solve”, and most of them solicit the reader’s curiosity and invite him to futher explore the related topics (plenty of references are given at the end of each chapter).

Chapter 23 explains a sane reduction between COL4 (the problem of deciding whether a graph is 4-colorable) to COL3 (the problem of deciding whether a graph is 3-colorable). Both are well known NP-complete problems. I started reading the chapter, but suddenly stopped and tried to figure out a reduction by myself.

The idea presented in the book is to replace each node of the graph $G$ of the COL4 problem with four nodes, force them to be colorable with colors F and T (the third color R is not allowed), force exactly one of them to be T, and finally adding a gadget that prevents two adjacent quadruples from having two corresponding nodes colored with T.

I came up with a very similar reduction, but the gadgets involved are slightly smaller: indeed a 4 colorable node can be represented “in binary” with two nodes each one colorable with T or F (two bits).

The construction to build a graph $G’$ that is 3-colorable if and only if the original graph $G$ is 4-colorable is the following.

Every node $n_i$ of the original graph $G$ is replaced with two nodes $n_i’$ and $n_i”$. We add a common triangle with three new nodes and an edge between its “Red” $R$ node and each $n_i’$ and $n_i”$, in this way all $n_i’, n_i”$ must be colored $T$ or $F$. Note that we simply label “red” the color assigned to the vertex of the common triangle that we connect to the nodes $n_i’, n_i”$ (in a valid coloring R,F,T are interchangeable) .

We replace each edge $e_h = (n_i, n_j)$ of $G$ with the edge gadget showed in the figure.

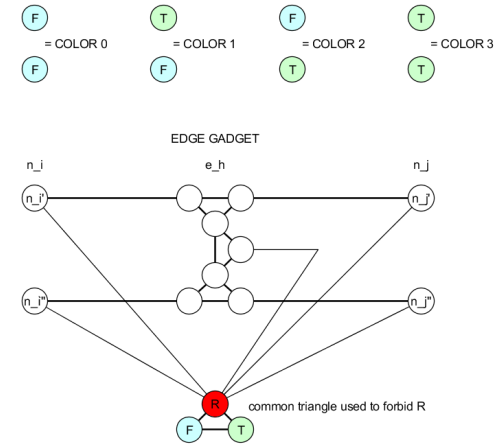
The edge gadget that replaces the original edge $e_h = (n_i, n_j)$ acts as a comparator between the two side: if $n_i’$ and $n_j’$ (resp. $n_i”$ and $n_j”$ ) have the same color, then one of the two inner nodes that connect them in the edge gadget must be red. As a consequence, if both $n_i’ = n_j’$ and $n_i” = n_j”$ then no node of the central triangle can be colored with red; note that red is already forbidden in the middle node of the central triangle because it is connected to the common $R$.

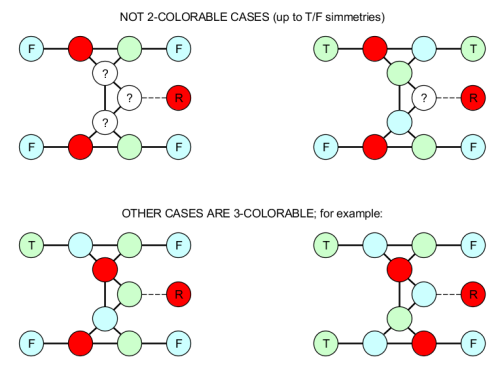
So the edge gadget is 3-colorable if and only if $(n_i’ \neq n_i”) \lor (n_j’ \neq n_j”) $. But the colors of $n_i’, n_i”$ represent the two bits of a 4 color so the edge gadget is 3-colorable if and only if in the original graph we can assign to $n_i$ and $n_j$ two different colors among the 4 available.

We can conclude that the whole resulting graph $G’$ can be 3-colored if and only if the original graph $G$ can be 4-colored.

A similar technique could be applied to the reduction $COL_a \leq COL_b$ when $a = 2^m$ expanding the edge gadget.

Open problem: is there a simpler $COL4 \leq COL3$ reduction ?