Recently A. Amarilli (a3nm) posted a question on cs.stackexchange.com about the computational complexity of a Test Round problem of the Google France #Hash Code 2015: the “Pizza Regina” problem (March 27th, 2015):

Definition [Pizza Regina problem]

Input: A grid $M$ with some marked squares, a threshold $T\in \mathbb{N}$, a maximal area $A \in\mathbb{N}$

Output: The largest possible total area of a set of disjoint rectangles with integer coordinates in $M$ such that each rectangle includes at least $T$ marked squares and each rectangle has area at most $A$.

The problem can be converted to a decision problem adding a parameter $k \in \mathbb{N}$ and asking:

Question: Does there exist a set of disjoint rectangles satisfying the conditions (each rectangle has integer coordinates in $M$, includes at least $T$ marked squares and has area at most $A$) whose total area is at least $k$ squares?

The problem is clearly in $\mathsf{NP}$, and after struggling a little bit I found that it is $\mathsf{NP}$-hard (so the Pizza Regina problem is $\mathsf{NP}$-complete). This is a sketch of a reduction from MONOTONE CUBIC PLANAR 1-3 SAT:

Definition [1-3 SAT problem]:
Input: A 3-CNF formula $\varphi = C_1 \land C_2 \land … \land C_m$, in which every clause $C_j$ contains exactly three literals: $C_j = (\ell_{j,1} \lor \ell_{j,2} \lor \ell_{j,3})$.
Question: Does there exist a satisfying assignment for $\varphi$ such that each clause $C_j$ contains exactly one true literal.

The problem remains NP-complete even if all literals in the clauses are positive (MONOTONE), if the graph built connecting clauses with variables is planar (PLANAR) and every variable is contained in exactly 3 clauses (CUBIC) (C. Moore and J. M. Robson, Hard tiling problems with simple tiles, Discrete Comput. Geom. 26 (2001), 573-590.).

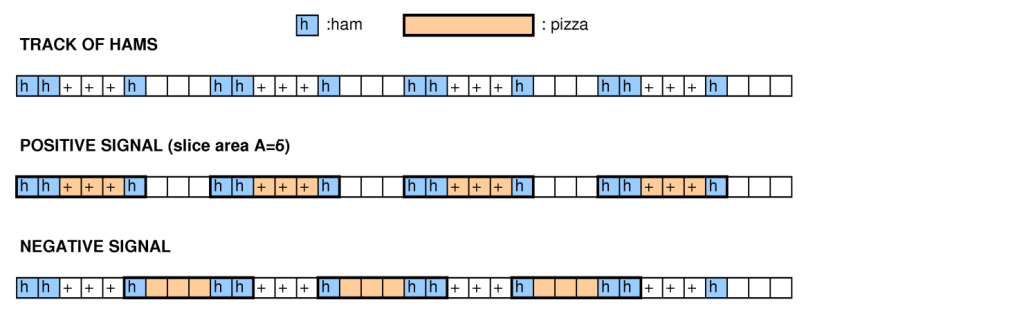
We use $T=3, A=6$, and in the figures ham is represented with blue boxes (transgenic ham?), pizza with orange boxes.

The idea is to use tracks of ham that carry positive or negative signals; the track is made with an alternation of 1 and 2 pieces of hams placed far enough so that they can be covered exactly by one slice of pizza of area $A$; the segments of the track are marked alternately with $+$ or $-$, the track will carry a positive signal if slices are cut on the positive segments:

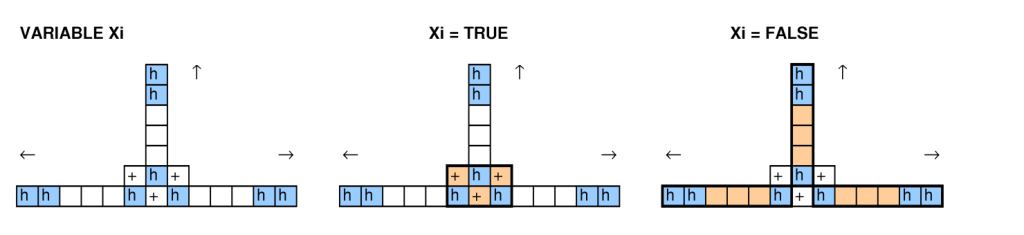
Each variable $x_i$, which is connected to exactly 3 SAT clauses, is represented by three adjacent endpoints of three ham tracks (positive segment), in such a way that there are 2 distinct ways to cut it, one will “generate” a positive signal on all 3 tracks (it reppresent the $x_i = TRUE$ assignment) the other a negative signal ($x_i = FALSE$). Notice that we can also generate mixed positive and negative signals, but in that case *at least one ham remains uncovered*.

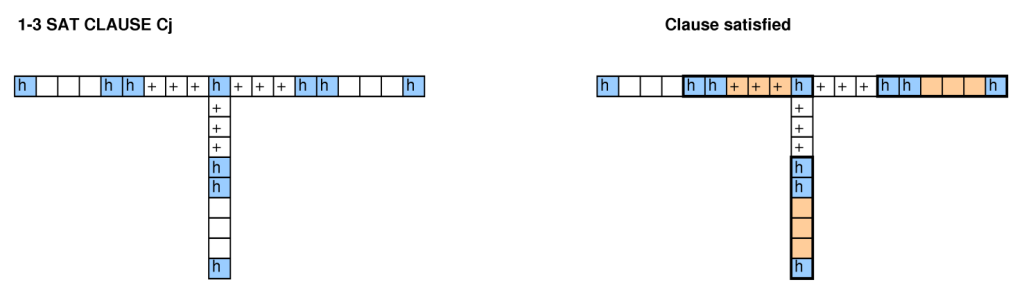
Each clause $C_j$ of the 1-3 SAT formula with 3 literals $L_{i,1}, L_{i,2}, L_{i,3}$ is simply represented by a single ham with three incoming positive segments of three distinct ham tracks; by construction *only one of the three tracks* carrying a positive signal can “cover” the ham-clause.

Finally we can build shift and turn gadgets to carry the signals according to the underlying planar graph and adjust the endpoints:

Suppose that the resulting graph contains $H$ hams. By construction every slice of pizza must contain exactly 3 hams, and in all cases every slice can be enlarged up to area $A$.

If the original 1-3 SAT formula is satisfiable then by construction we can cut $H /3$ pieces of pizza (with total area of $A H / 3$) and no ham remains uncovered.

On the oppposite direction, if we can cut $H /3$ pieces of pizza (with total area $A H / 3$) then no ham remains uncovered, and the signals on the variables gadgets and on the clauses are consistent: the ham on the clause is covered by exactly one positive slice coming from a positive variable, and every variable generates 3 positive signals or 3 negative signals (no mixed signals); so the cuts induce a valid 1-3 SAT assignment.

Conclusion: … so unless $\mathsf{(P)izza} =\mathsf{(NP)izza}$, cutting a pizza can be really hard. I would like to thank Antoine for posting the funny question and for spending a bit of time checking my proof.